You are here - OLRC Home   |   Site Index   |   Contact Us
			Go to.... - OLRC Home - About Us - Aspire - Projects - Publications - News & Events

Algebra: Patterns and Functions
The area of algebra, both formal and informal, presents a challenging dilemma, because although educators wanted this included, learners often react in a negative manner, with personal stories of frustration and agony. When adults reflect upon what it means to do algebra, they tend to recall formal methods of equation solving, age problems, and lots of X's and Y's. But mathematics educators at all levels have begun a dialogue with a very different emphasis on conceptual understanding, on algebra as a means of representation, and on algebraic methods as a problem solving tool. They are not talking about the mechanical high school algebra but algebraic reasoning that allows us to think about and express patterns, relations and functions and which ultimately gives many more people access to technology.

Many frustrations are connected to past experiences with algebra. Many adults site algebra as a major stumbling block in their earlier math education, the place where they got stuck. Whatever the reason, many learners report an incredible disconnect at the point where algebra is traditionally introduced.

There is a widely held notion that algebra is not practical, relevant or useful. Yet algebra is a bridge between arithmetic and more broadly generalized mathematical situations. Mathematics is the study of patterns. These generalizations can be expressed in the notation of formulas and graphs. Many life and work experiences can be expressed in algebraic terms. While most learners do not see the relevancy of algebra, and many teachers see the academic relevancy, employers and other workers do see the application to today's workplace. Life experience should afford adult basic education teachers with a broad base of real-world ties which can be readily linked to the concepts of equation, function, variable and graph.

Algebraic thinking skills are crucial if adults are to compete in the global economy: therefore all adult learners should have the opportunity to improve in that area. Algebra impacts the competency of workers, parents and citizens. While basic skills are obviously important, it is also useful to have working knowledge of algebraic language. This way of thinking, critically and analytically, contributes to one's daily thought process. Any adult who can think more systematically and analytically is bound to be a better citizen, worker and parent. Better thinkers think ahead. Thinking algebraically influences all areas of our lives.

IMPLICATIONS FOR LEARNING AND TEACHING
It is necessary to introduce all learners to algebraic concepts by making links to the learner's experiences.

We must pay attention to instructional pace, vary teaching strategies and strengthen the development of concepts to improve algebra instruction. It has been suggested that the source of trouble might have to do with the pace of the instruction. Learners, too, need time to assimilate the material and reflect upon it.

Stressing logic puzzles, "function machines", tables and graphs, as well as the concept of what an equation really means are all strategies to help build algebraic thinking.

Graphs and Charts
LARGE GROUP:

Discuss:

What is the purpose of a graph or chart?

quick impression

picture display of information

good way to compare information, draw conclusions

drawn rather than written

Individual:
Demonstrate: Real Graph/ Symbol Graph/ Bar Graph
Pass out 10 tiles to each member of the group.

1. Each member separates and counts the tiles by color.

2. Line them up by color so they make column.

3. Compare the columns.

4. You made a real graph, from real objects.

5. What symbol can we use to represent a tile?

6. Make a graph using the symbol to show how many tiles.

7. Instead of symbols, we can use a bar to show the number of tiles.

8. Draw bars showing the number of tiles. Do your bars go up and down? That is a vertical bar graph. If they go across, that is a horizontal bar graph.

Small Group:

Demonstrate

Circle Graph
Circle graph compares parts of a whole, line graph shows trends

1 . How many total tiles do we have? How many tiles do we have? (Again, this count can be taken individually, small group and large group to reinforce process)

2. The total goes on the bottom and the :red goes on the top.

3. Take number of green tiles over the total.

4. Take the number of black tiles over the total.

5. Make a circle and divide according to fraction. (Hint, you can also convert to percent by dividing the total into the number of colored tiles.)

Large Group:
1. Get information from each group and demonstrate process with results from whole class.

Small group Demonstrate: Line Graph

1. Select a recorder to write down the number of red tiles that each student has, the number of black tiles each student has and the number of green tiles each student has.

2. Now, pass out markers, graph paper, and pencils to each group.

Discuss in Large group
Let's look at the things necessary to make a line graph.

We need:

A title
A constant
A variable.

Where can they be found?

Large Group:

Coordinates

Discuss:

1. Go to the line graphs and read the next point about Cartesian plane,

2. It's the graphing of points on a plane that allows us to draw graphs or pictures of algebraic expressions.

3. The coordinate plane is the grid (graph paper). Pass out another sheet.

4. The numbers that name the intersection are called ordered pairs. For example, the ordered pair (3,2) names third across, second down.
Always read horizontal, then vertical.

5. These intersections are called points. The ordered pair is always shown in parenthesis.

6. The coordinate plane (grid) has a horizontal plane and a vertical plane which is numbered.

7. The point at which the axis meet is called the origin.

Demonstrate:

1. Draw a grid on the board ( 3 by 3)

2. Plot (1, 1) =A, (1,3)=B, (2,3)=C, (3,2)=D and explain intersection and points as you go. Remember: horizontal then vertical

3. Now let the class draw a 3 by 3 on paper and plot the following:

E= (2,2), F= (3,3), G = (1,2), H= (2, 1)

Cartesian plane using both positive and negative numbers

1. So far we've worked with only positive numbers. Can you think of instances where both positive and negative numbers may be used?

2. Pass out graph paper.

3. Draw a cross on the board and label 1,2,3, both positive and negative.

4. Show the 4 Quadrants in this graph instead of 1.

5. Plot I= (- 1, 1), J= (3,-2), K= (-2,3) L-- (-3, 1) horizontal then vertical

6. Now, it's your turn. Plot M= (1,- 1), N= (2,3), O= (3,- 1), P= (-2,-3)

Small Group

1 . Coordinate Tic Tac Toe: Ask group to divide into groups of 2 to play tic, tac toe. Start them off with your naming the numbers and they plot.

2. After you have demonstrated how this works, they should be able to play with each other for about 5 minutes.

1. Hurkle: Pass out more paper. Leader decides where Hurkle is.

2. Leader announces "Hurkle is hiding on a point.

3. Group guesses

4. Give dues, N,S,E,W,SW,NE, etc.

5. First team to guess location wins.

ALGEBRA News
Combining Positive Negative Numbers
Use playing card language.

+ + same day		+ -mixed up day
- - good day		+ - bad day
	or

(+8) (+4) 1 can go to the store.		= +
(-8) (+4) 1 cannot go to the store.		= -
(+8) (-4) Yes, I cannot go to the store.		= -
(-8) (-4) No, I cannot go to the store.		= +

Balancing Equations

Hold up both hands - Are they equal?
Add two pencils to the right hand - Are they equal?
How do you make it equal?

Algebra as a game

Know the rules-
Rule 1 - Set up problem
Rule 2 - Combine like terms
Rule 3 - Inverse operations
A. Multiply and/or divide first
B. Add and/or subtract second

Order of Operations Acronym

Please Excuse My Dear Aunt Sally
parentheses, exponents, multiplication and division, addition and subtraction

Simplify: 6(8 - 11) + 2

Parentheses 6( -3 + 2
Exponent 6( -3 + 8
Multiply -18 + 8
Add -10

ALGEBRA NEWS
Multiplication of Polynomials

FOIL Method




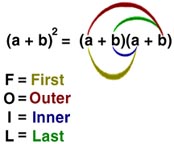
PICTURE Method




Regular Multiplication

Setting Up Word Problems
READ - Do you add, subtract, multiply, or divide? Who or what is involved? Change names to f ones.

READ - Who or what do you know nothing about?

READ - Read backwards in phrases.

EXAMPLE: A contractor needs to order windows for a building she is constructing, The building has four sides and each side requires 53 windows. How many windows will be needed?

Algebra GLOSSARY

ALGEBRA

The study of expressions containing variables.

ALGEBRAIC EXPRESSIONS

Two or more numbers or variables combines by addition, subtraction, or multiplication. (I.e. X + 6 = or 3/5 =)

EQUATION

A mathematical sentence written with symbols. A mathematical sentence can be true or false. A SOLUTION makes the equation true. Any other value makes the equation false.

EXPONENT

Tells how many times a number is multiplied by itself

"LIKE TERMS"

Terms that have exactly the same variable parts. (i.e. 2X, 5X, 1/2X = like terms)

NEGATIVE NUMBERS

Those numbers smaller than zero.

NUMBER LINE

Looks like a thermometer scale on its side. Negative numbers you solve that which is in parenthesis (if there is more that one set, work from the inside out), then work the exponents, then the multiplication then the division, then the addition and subtraction.

POLYNOMIAL

A special kind of algebraic expression. A polynomial has one or more terms combined by addition or subtraction.
A polynomial with one term = nomial.
A polynomial with two terms = binomial.
A polynomial with three terms = trinomial.

POSITIVE NUMBER

Those numbers larger than zero.

"UNLIKE TERMS"

Terms that have different variable parts. (i.e. 3X and 7Y unlike terms)

VARIABLES

Letters that stand for an unknown numerical value that changes from problem to problem. (i.e. X + 13 = 25 or 8 - X = 4)

BIBLIOGRAPHY
Compton's Interactive F-Encyclopedia. Compton's NewMedia Inc., 1994.

Laycock, Mary and Margaret A. Smart. Manipulative Interludes Algebra. Activity Resources Company, Inc., 1990.

Saunders, Hal. When Are We Ever Gonna Have to Use This?. Dale Seymour Publications, 1988.

Stenmark, Jean Kerr, Virginia Thompson, and Ruth Cossey. Family Math. University of California Regents, 1986.

Back to Contents Page

		Return to the Top
	This page http://literacy.kent.edu/Oasis/Resc/Educ/algebra.html and is maintained by the OLRC . Follow us on