You are here - OLRC Home   |   Site Index   |   Contact Us
		Go to.... - OLRC Home - About Us - Aspire - Projects - Publications - News & Events

Title:

Measuring Fences - Understanding Perimeter

Materials:

Squares, rectangle, and triangles of different sizes cut from cardboard or construction paper, or a copy of Handout 1; two sizes of paperclips

Audience:

Adult learners with low to intermediate math skills

Setting:

Classroom or tutor situation; group or one-on-one

Activity:

In a discussion with students, relate perimeter to a fence in that they both surround a space on all sides; learners are more likely to remember to include all sides when finding perimeter if you continually refer to the fence concept.

Provide students with the figures of differing sizes and about 20 of the smaller paperclips; have them determine how many paperclips it takes to go around each figure. Compare findings to verify that all students are measuring correctly. Make the connection that what they have measured is the perimeter of the figure.

Next, give learners about 10 jumbo paperclips and ask the following questions:

1.) Will it take the same number of the larger paperclips to make the perimeter of the figures as it did the smaller clips? (no)

2.) Will it take more or fewer of the larger clips? (fewer)

Tell students to prove their answer to question 2 by using Jumbo clips to measure the perimeter of one of the figures.

Then ask:
3.) Why did it take fewer large paperclips than smaller paperclips to make the perimeter of the figure? (allow all answers; verify the correct answer with the continuation of the exercise)

Show the class a well used pencil and an unsharpened pencil, then ask:

4.) Would it take more of the new pencil or more of the used pencil to measure the perimeter of the top of my desk? (more used pencil because it is smaller)

Repeat this using two sizes of other objects (straws, toothpicks, pens, craft sticks) and measure other objects in the room until the learners conclude that it always takes fewer larger units than smaller units to measure the same distance. Conclude by asking the same question about inches and feet; feet and yards; and any other standard units desired.

Evaluation:

This hands-on activity reinforces the fact that perimeter measures the distance around a figure and that it takes fewer large units than small units to measure equal distances.

Modification:

Use actual items in the classroom to measure. After the activity, measure the perimeter of the classroom using a ruler, then repeat using a yard stick. Discuss the relationship of the outcomes with the number of feet in a yard.

Title:

Making Fences - introducing the Formula for Perimeter

Materials:

About 20 straws for each pair of students (if space is limited use bar straws or craft sticks)

Audience:

Adult learners with low to Intermediate math skills

Setting:

Classroom or tutor situation; group or one-on-one

Activity:

A: Perimeter of a square

Distribute about 20 straws to each pair of students; ask them to use some of their straws to make a square. Walk around to ensure that all students are proceeding correctly. Then ask:

1.) How many straws did you use to make your square? (answers may vary)

Connect this to the fact that the number of straws used to make the square is the perimeter of the square. Next instruct learners to make a square with a perimeter of 8 straws; check that all have succeeded-. Then ask them to make a square with a perimeter of 10 straws. They will not be able to comply unless straws are cut which is not allowed. Ask:

2.) Why couldn't you make a square with a perimeter of 10? (accept all answers and verify the correct answer by continuing the activity)

Continue the activity by requesting that learners make squares with other perimeters, mixing in some that are not -possible. (4, 61 12, 15, 16, 18, 20) Learners should come to the conclusion that all possible perimeters are multiples of four. Introduce the formula for the perimeter of a square, P = 4s (perimeter equals four times the side of the square).



B. Perimeter of a rectangle Ask students to make a rectangle using some of their straws. Then ask: 3.) How is the rectangle different than the squares you made? (it is longer one way than it is the other way)

Repeat the activity above Instructing students to make rectangles of various perimeters. The smallest perimeter using whole straws is six, and all perimeters will be multiples of two. Lead the students to this discovery through the construction of the rectangles.

Introduce the formula for the perimeter of a rectangle, P 21 + 2w (perimeter equals two times the length plus two times the width). It is because you always have to multiply the length and width times two that the perimeter is a multiple of two. (This Is true only when using whole units as dimensions.)



C. Perimeter of a triangle

Repeat the activity having the students construct triangles. Lead the students to discover that there is no requirement for the perimeter of a triangle except that there be only three sides. Introduce the formula for perimeter of a triangle, P = a + b + c (perimeter equals side a, plus side b, plus side c.)

Evaluation:

A hands-on activity to discover the origin of the formulas for perimeter. This type of 'discovery usually helps the student to retain the formulas in memory.

Modifications:

This should be accomplished in a series of classes beginning each new session with a review of concepts already learned. If the class is high intermediate, the concepts of the right triangle could be explored (i.e. the side opposite the right angle is always the longest).

Title:

Two Bits Square - Understanding Area

Materials:

Quarter-size circles and one-inch squares of heavy paper or cardboard; a copy of Handout 1 for each pair of students

Audience:

Adult learners with low to intermediate math skills

Setting:

Classroom or tutor situation; group or one-on-one

Activity:

Begin by distributing copies of Handout 1 and about 25 circles and 25 squares to learners. Then ask:

1.) How many quarters do you think would cover figure A? (accept all answers; verify correct answer as activity continues)

Next have learners actually cover figure A with the quarter size circles to verify correct number. Repeat with figures B and C, having learners first estimate how many before covering the area. Explain that the area is the covering of the surface of a figure. Then ask:

2.) How many of the one-inch squares do you think It would take to cover figure A? (accept all---answers; verify answer as activity continues; it will take the same number of squares as circles)

Have learners cover figure A with one-inch squares to verify the correct number. Repeat with figures B and C, estimating the number before covering figure. They should discover that the number of quarters is the same as the number of square inches.

Evaluation: This activity can help learners gain a reference for estimating square inches by visualizing quarters.

Modification: Have students estimate how many quarters would cover items on their desks or in the class. Intermediate to high level learners could perform the activity using figures D and E or with figures on Handout 2.

Title:

Grazing the Pasture - Measuring Area

Materials:

Handout 1; a transparency of the one-inch grid sheet for each pair of learners; surfaces or faces of several classroom items

Audience:

Adult learners with low to intermediate math skills

Setting:

Classroom or tutor situation; group or one-on-one

Activity:

Discuss with learners that area is like a pasture or vacant lot: it covers a flat space. For that reason it is measured with a flat measurement such as square inches.

Have learners lay transparencies over figure A of Handout 1 and count the number of squares it takes to cover the area. Reinforce the fact that area is always measured in square units. Learners can then measure the area of figures B and C. More advanced learners can find the area of figures D and E (the triangle and circle). The transparencies can be written on with china marker's or overhead markers to help students count squares at outline the figures.

Let students use the transparencies to find the area of some items in the classroom such as book covers, window panes, table tops, etc.

Evaluation:

This hands-on practice reinforce the fact that area covers a flat space, not a linear distance, and must be measured in square units.

Modification:

Measure area using a transparency of the half-inch square grid as a follow up activity. Ask learners first if they expect It to take more or fewer half-inch squares than one inch squares to cover each area. After they discover that It takes more half-inch squares to measure every area, reinforce that it always takes fewer large units than small to cover the same area.

On a clear shower curtain liner, have students make a square-foot grid using a T-square, tape measure, and permanent markers. Measure the area of large classroom surfaces available such as table tops, blackboards, walls, or floors. (This grid can later be used to teach latitude and longitude by numbering the lines.)

Title:

Greener Pastures - Introducing the Area Formula

Materials:

Handout 1; square-inch grid transparencies; rulers

Audience:

Adult learners with low to intermediate math skills

Classroom or tutor situation; group or one-on-one

Activity:

This activity should follow Grazing the Pasture. After measuring many surfaces using the transparency, the learner needs to understand that it is not the Simplest nor the conventional way to find area. It would be cumbersome to carry with you sheets to lay on surfaces and tedious to have to count the squares.

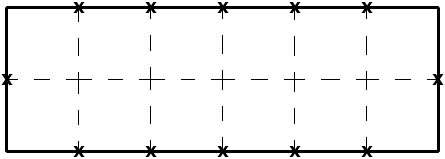
Ask students to measure each side of figure A and mark off each inch. Next have them connect the marks opposite each other. (You may have to show an example of this on the board. )

Example:


Then ask:
1.) How many squares are in figure A? (12)

2.) What was the area when you measured It with the transparency grid? (12 square units (or inches))

After naming the longer side the length and the shorter side the width, ask:

3.) How many inches did you mark off an the length (across the top) of figure A? (6)

4.) How many inches did you mark off on the width (along one side) of figure A? (2)

Instruct students to multiply the number of inches across the top of figure A by the number of inches along the side of figure A. Ask:

5.) What number do you get when you multiply these two numbers? (12)

6.) What conclusion can you make from this? (that to find area you can multiply the length of the rectangle by the width of the rectangle)

Repeat this process with figures B and C. You have Just proven the formula for the area of a rectangle, A = lw (area equals length times width).

Title:

Half a Pasture - proving a Formula for Area of a Triangle

Materials:

Two copies of Handout 1; rulers; scissors; square inch grid transparencies per pair of students

Audience:

Adult learners with low to intermediate math skills

Setting:

Classroom or tutor situation; group or one-on-one

Activity:

Have learners find the area of figure B, then draw a diagonal line from one corner to the opposite corner in the figure. You may need to show an example on the board.

Example:


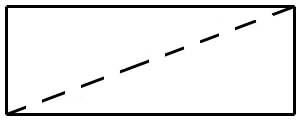
Tell learners to cut out figure B. When they have done this, have them cut on the diagonal line. Then ask:

1.) What do you have now that you have cut along the diagonal line? (two triangles)

2.) How do the triangles compare in size? (they are the same)

Lead students to see that they have cut the rectangle In half; therefore, the area of each triangle is half of the area of rectangle B by asking:

3.) What Is the area of one of the triangles? (6 square .inches)

Let students use transparencies to confirm the area of the triangle.

Going back to the uncut copy of Handout 1, have students rename the width the base (because the figure sits on it) and the length the height (because that is how tall the figure is). Ask:

4.) What number do you get if you multiply the base times the height? (12)

5.) How does this compare with the area of figure B? (it is the same)

6:) Why is It the same? (because the base and height are the same as the length and width, and area equals length times width)

7.) What is half of this area? (6 square inches)

8.) How does this compare with the area of one of the triangles that you made from figure B? (it is the same)

9.) Why? (because one triangle is half of the rectangle)

Introduce the formula for the area of a triangle, A = 1/2 bh (area equals half of the base times the height OR area equals one half times the base times the height).

Evaluation:

This hands-on proof should make it easier for learners to remember to use the one-half in the formula for the area of a triangle; this is often a problem for students.

Modification:

It may be necessary to repeat the activity using figures B and C for some students to grasp the concept. Repeating the hands-on process is usually helpful for slower learners.

Title:

Do Equal Pastures Have Equal Fences? - The Relationship Between Perimeter and Area

Materials:

12 square-inch tiles and copy of Handout 5 per pair of students

Audience:

Adult learners with low to intermediate math skills

Setting:

Classroom or tutor situation; group

Activity:

Distribute 12 square-inch tiles to each pair of learners. Instruct learners to make a figure with an area of 2 square inches making sure that whole sides touch



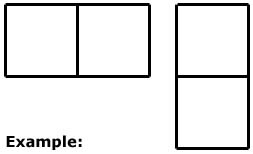
Have students find the perimeter of their figure and fill in the appropriate numbers In the chart on Handout 5. At this point all areas and perimeters will be the same.

Ask students to make a figure with an area of three square Inches. This could provide some variety In the look of the figures and in the perimeters. However, they may all have the same results. Students then add the information to their chart.

Continue to increase the area of the figure you ask the students to make up to twelve square inches in area, having them record the information on their charts each time.

Conclude the activity by making a classroom chart showing all of the results from all of the learners' figures. It should then be very clear that the same area does not mean the same perimeter.

Evaluation: This activity can inspire a lot of discussion about the shapes that can produce the same area. It also very effectively makes the point that same area does not mean same perimeter.

Modification: You can use a combination of squares and rectangle (doubles or triples of the squares used) and even right triangles for more advanced students.

This is also a great way to explore the multiplication facts. If you do not allow any shapes other than squares and rectangles, the lengths and widths will be the factors of the areas In every case.

Title:

Equal pastures, Equal Fences? . (Version 2)

Materials:

Rectangular sheets of construction paper; scissors

Audience:

Adults learners with math intermediate to high math skills

Setting:

Classroom or tutor situation; group or one-on-one

Activity:

Distribute one piece of construction paper to each learner. Have learners draw a diagonal line from one corner to its opposite corner, then cut on the line producing two triangles. Have them mark inches along the edges as a guide to determine perimeter.

Instruct each learner to construct as many figures as possible (3) by placing matching sides of the triangles together. They should draw a sketch of each figure and find Its perimeter; then compare the perimeters. Be sure they realize that the area of every figure is the same because that one piece of paper was used.

The outcome should be that while the areas are the same, the perimeters are different.

Evaluation:

This is a quick activity especially good for intermediate to high level students to show that the same area does not always mean the same perimeter.

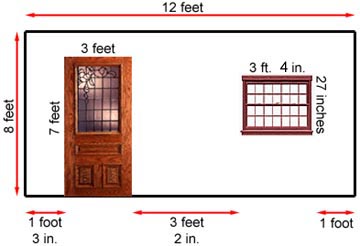
What is the least number of rolls of wallpaper you will need to wallpaper the wall shown above? The wallpaper is sold in rolls 24 inches by 25 feet. You do not need to match a pattern but all seams must be up and down.

Title:

Post-It Note Area

Objective:

To develop an intuitive understanding of the concept of area To practice measuring "unit areas"

Materials:

Post-it Notes (square pads)

Audience targeted level:

Literacy, pre-GED® or GED

Type of setting:

Classroom, small group or one on one

Time required:

20-30 minutes

Activity:

Students should estimate the number of Post-It Notes it would take to cover a surface. Possible surfaces: notebook cover, folder, desk top, book, or table top. Next, use Post-it Notes to actually cover the area. In this way students can actually experiment with a square unit. Compare the actual number of Post-It Notes required with the estimate.

Questions:

How do the estimate and the actual count of Post-It Notes compare? What happens when Post-It Notes don't fit?

Evaluation:

This activity gives students hands on experience understanding the concept of area and square units.

Recommended Resources:

Modifications:

This same activity could be done with paper, scissors and glue. Objects in the classroom could be traced on newspaper. Students could cut squares of a determined size (not necessarily a square inch) from scrap paper. These squares could then be glued on the newsprint.

Title:

Wrap, Wrap, Wrap!

Objective:

To introduce students to geometry. To practice measuring skills. To understand the concepts of length, width, height, volume and surface area. To develop problem solving skills.

Materials:

Rulers, tape, scissors, 15 small to medium size boxes per group (Small boxes are most desirable. Individual size cereal boxes, plastic cassette tape containers, earring boxes are recommended), and a sheet of 36" by 30" wrapping paper = group. (Rolls of paper can be cut to equal a similar quantity of paper. Large sheets of paper can be found at paper outlet stores.)

Audience targeted/level:

Multilevel (1, 11, M)

Type of setting:

Students are grouped into three or four per group.

Time required:

1 1/2 hours, depending on the length of introduction to the concepts and formulas for volume and surface area.

Activity:

All students are introduced to the concept and formula for volume and surface area. Students are then grouped into small groups of 3 to 4 students. Each group chose a person to lead, measure, cut and tape. The leader chooses a piece of wrapping paper. Then the teacher poses the problem: "There's going to be a baby shower. You were chosen to buy all the gifts with the money that has been given to you by your classmates. You were so busy shopping that when you got home, you noticed you had hardly anytime to wrap the presents Even worse, you discovered that you had 1 sheet of paper to wrap all the presents. That is your problem." Students are advised that prizes will be given to the group that wraps the most presents and/or the group with the least waste. Next the leaders come up, and one at a time, pick one box at a time until every leader of a group has 10 boxes. Be careful that a leader doesn't pick more than one. Leaders must take consecutive turns to be fair. Start wrapping. No splices are allowed. All sides of boxes have to be completely covered. After a group has wrapped at least 10 boxes, the leader may go up and choose another box to wrap. When that box is wrapped, the leader may choose another one, and so on, but only one at a time.

To measure the group who has the least waste, introduce the area formula and compare the waste of the groups.

Prizes should be given to the whole class as well as something extra for the winners.

Evaluation:

This activity was lots of fun for the students. The group which won (14 boxes wrapped) in the test class was the group with the lowest level students.

Modifications:

The problem could be changed to reflect the interests of the class.

Title: Tangram Unit Area

Objective:

To develop an intuitive understanding of the concept of area. To practice measuring in "unit areas"

Materials:

Tangrams, Tangramath worksheets, pp. 24, 25, 62, 63, 64 and 65 or similar sheets. See sample below

Audience targeted/level:

Literacy, pre-GED® or GED

Type of setting:

small groups, pairs or individuals

Time required:

20 minutes

Activity:

Use the Tangramath worksheets and the tangrams to compare the sizes (areas) of two differently shaped drawings. Use the tangram small triangle to measure the areas of the other tangram pieces. Measure some areas using tangram triangles or squares.

Evaluation:

Recommended Resources:

Tangramath, Creative Publications (available through Dale Seymour)

Title:

Identify the Angles

Objective:

To identify right, acute, and obtuse angles using pattern blocks

Materials:

Pattern blocks for student use

Audience targeted/level:

All levels

Small groups or one on one

Time required:

10 to 15 minutes

Activity:

Using pattern blocks students will find a shape or shapes that has...
... only right angles
... only acute angles
... only obtuse angles
... find three shapes that have two acute angles and two obtuse angles
(identify which angles are acute and which are acute)

Evaluation:

This was a fun activity for the students and a quick hands on way to identify types of angles.

Recommended Resources:

Modifications:

A similar line of questioning could be used with tangrams.

Title:

Angles, Angles, Angles!

Objective:

To introduce the students to angle relationships.

Materials:

Pattern blocks for the class

Audience targeted/level:

All levels of ABLE students

Type of setting:

This activity works well when done in pairs or small groups. It could be done individually.

Time required:

30 minutes

Activity:

Introduce the concept of complementary angles. Find two pattern block shapes that have comers that make complementary angles when matched up. Use a shape with a 90 degree angle (the orange square) to prove your answer. How many different combinations of shapes will make complementary angles? (3)

Introduce the concept of supplementary angles. Find two pattern block shapes that will make supplementary angles when their comers are matched up. How many combinations can you find? (9)

Introduce the concept of vertical angles. Arrange four trapezoids from the pattern block set to show two intersecting lines. (See drawing 1) Use two green triangles lined up over the acute vertical angles to show they have equal measures. (See drawing 2) Two blue parallelograms lined up over the obtuse angles will demonstrate the equal measures of those angles.

Introduce the concept of parallel lines cut by a transversal. If another row of trapezoids is added to the previous drawing, a set of parallel lines cut by a transversal will be created. Using the green triangles and blue parallelograms to "measure" again, these relationships can be explored.

Evaluation:

This activity was fun and interesting for the students.

Recommended Resources:

Modifications:

The concepts of complementary and supplementary angles could be explored using tangrams but there are fewer combinations.

Title:

180 Degrees - Yes, No, or Maybe

Objective:

To prove that the sum of the angles in a triangle is 180 degrees.

Materials:

Paper, rulers, scissors and glue.

Audience targeted/level:

All ABLE students, no matter what their math level

Type of setting:

Group or individual activity

Time required:

20 to 30 minutes

Activity:

Review the meaning of supplementary angles and straight angles. Review the various types of triangles. With paper, pencils and rulers the students will construct various types of triangles. In order to later identify the angles of the triangle students need to mark each comer or angle. Tear the triangle in three pieces so each piece contains an angle. (Tearing the paper makes it easier to identify the original angles.) The angles are then glued on another sheet of paper so the middle angle joins each of the other two at a side and the vertices meet at a point.

Discuss the shape that the three angles form. What does this mean? What can be concluded about the sum of the angles in different shaped triangles?

Evaluation:

This hands-on activity makes the concept of the sum of the angles in a triangle very clear to the students. They really remember that there are 180 degrees in the sum of the angles.

Title:

Fun With Polygons

To understand polygons

Materials:

Pattern blocks

Audience targeted/level:

All ABLE levels

Type of setting:

Small groups

Time required:

Minimum of 15 minutes

Activity:

Using pattern blocks construct various polygons (hexagons, triangles, quadrilaterals, pentagons, etc.) Students can construct a shape and then identify it or choose a shape to construct. The shapes can be compared for similarity.

Evaluation:

Modifications:

Back to Contents Page

		Return to the Top
	This page http://literacy.kent.edu/Oasis/Resc/Educ/geometry2.html and is maintained by the OLRC . Follow us on